一阶保持（First-order hoId,FOH）是一种重建信号的数学模型，可以透过传统的数位类比转换器(DAC)及称为积分器的模拟电路完成。

基本的一阶保持

　　一阶保持是利用假想的滤波器或是线性时不变系统，将理想的取样讯号

　　{\displaystyle x_{s}(t)\,}{\displaystyle x_{s}(t)\,}{\displaystyle=x(t)\T\sum _{n=-\infty}^{\infty}\delta(t-nT)\}{\displaystyle=x(t)\T\sum _{n=-\infty}^{\infty}\delta(t-nT)\}

　　{\displaystyle=T\sum _{n=-\infty}^{\infty}x(nT)\delta(t-nT)\}{\displaystyle=T\sum _{n=-\infty}^{\infty}x(nT)\delta(t-nT)\}

　　转换为分段线性的讯号。

　　{\displaystyle x_{\mathrm{FOH}}(t)\,=\sum _{n=-\infty}^{\infty}x(nT)\mathrm{tri}\left({\frac{t-nT}{T}}\right)\}{\displaystyle x_{\mathrm{FOH}}(t)\,=\sum _{n=-\infty}^{\infty}x(nT)\mathrm{tri}\left({\frac{t-nT}{T}}\right)\}

　　所得到的等效冲激响应为

　　{\displaystyle h_{\mathrm{FOH}}(t)\,={\frac{1}{T}}\mathrm{tri}\left({\frac{t}{T}}\right)={\begin{cases}{\frac{1}{T}}\left(1-{\frac{|t|}{T}}\right)&{\mbox{if}}|t|<T\\0&{\mbox{otherwise}}\end{cases}}\}{\displaystyle h_{\mathrm{FOH}}(t)\,={\frac{1}{T}}\mathrm{tri}\left({\frac{t}{T}}\right)={\begin{cases}{\frac{1}{T}}\left(1-{\frac{|t|}{T}}\right)&{\mbox{if}}|t|<T\\0&{\mbox{otherwise}}\end{cases}}\}

　　其中{\displaystyle\mathrm{tri}(x)\}{\displaystyle\mathrm{tri}(x)\}是三角形函数

　　等效频率响应是冲激响应的傅里叶变换

　　{\displaystyle H_{\mathrm{FOH}}(f)\,}{\displaystyle H_{\mathrm{FOH}}(f)\,}{\displaystyle={\mathcal{F}}\{h_{\mathrm{FOH}}(t)\}\}{\displaystyle={\mathcal{F}}\{h_{\mathrm{FOH}}(t)\}\}

　　{\displaystyle=\left({\frac{e^{i\pi fT}-e^{-i\pi fT}}{i2\pi fT}}\right)^{2}\}{\displaystyle=\left({\frac{e^{i\pi fT}-e^{-i\pi fT}}{i2\pi fT}}\right)^{2}\}

　　{\displaystyle=\mathrm{sinc}^{2}(fT)\}{\displaystyle=\mathrm{sinc}^{2}(fT)\}

　　其中{\displaystyle\mathrm{sinc}(x)={\frac{\sin(\pi x)}{\pi x}}\}{\displaystyle\mathrm{sinc}(x)={\frac{\sin(\pi x)}{\pi x}}\}是正规化的Sinc函数。

　　可以令s=i 2πf，得到FOH传递函数的拉普拉斯变换：

　　{\displaystyle H_{\mathrm{FOH}}(s)\,}{\displaystyle H_{\mathrm{FOH}}(s)\,}{\displaystyle={\mathcal{L}}\{h_{\mathrm{FOH}}(t)\}\}{\displaystyle={\mathcal{L}}\{h_{\mathrm{FOH}}(t)\}\}

　　{\displaystyle=\left({\frac{e^{sT/2}-e^{-sT/2}}{sT}}\right)^{2}\}{\displaystyle=\left({\frac{e^{sT/2}-e^{-sT/2}}{sT}}\right)^{2}\}

　　因为一阶保持滤波器的冲激响应在t小于0时就已有值，因此此系统是反因果系统。

延迟一阶保持

　　延迟一阶保持（Delayed first-order hold）有时也称为因果一阶保持（causal first-order hold）和一阶保持相同，但输出会延迟一个取样周期才输出，因此会有延迟的分段连续信号

　　{\displaystyle x_{\mathrm{FOH}}(t)\,=\sum _{n=-\infty}^{\infty}x(nT)\mathrm{tri}\left({\frac{t-T-nT}{T}}\right)\}{\displaystyle x_{\mathrm{FOH}}(t)\,=\sum _{n=-\infty}^{\infty}x(nT)\mathrm{tri}\left({\frac{t-T-nT}{T}}\right)\}

　　其等效冲激响应为

　　{\displaystyle h_{\mathrm{FOH}}(t)\,={\frac{1}{T}}\mathrm{tri}\left({\frac{t-T}{T}}\right)={\begin{cases}{\frac{1}{T}}\left(1-{\frac{|t-T|}{T}}\right)&{\mbox{if}}|t-T|<T\\0&{\mbox{otherwise}}\end{cases}}\}{\displaystyle h_{\mathrm{FOH}}(t)\,={\frac{1}{T}}\mathrm{tri}\left({\frac{t-T}{T}}\right)={\begin{cases}{\frac{1}{T}}\left(1-{\frac{|t-T|}{T}}\right)&{\mbox{if}}|t-T|<T\\0&{\mbox{otherwise}}\end{cases}}\}

　　其中{\displaystyle\mathrm{tri}(x)\}{\displaystyle\mathrm{tri}(x)\}为三角形函数.

　　等效频率响应是冲激响应的傅里叶变换

　　{\displaystyle H_{\mathrm{FOH}}(f)\,}{\displaystyle H_{\mathrm{FOH}}(f)\,}{\displaystyle={\mathcal{F}}\{h_{\mathrm{FOH}}(t)\}\}{\displaystyle={\mathcal{F}}\{h_{\mathrm{FOH}}(t)\}\}

　　{\displaystyle=\left({\frac{1-e^{-i2\pi fT}}{i2\pi fT}}\right)^{2}\}{\displaystyle=\left({\frac{1-e^{-i2\pi fT}}{i2\pi fT}}\right)^{2}\}

　　{\displaystyle=e^{-i2\pi fT}\mathrm{sinc}^{2}(fT)\}{\displaystyle=e^{-i2\pi fT}\mathrm{sinc}^{2}(fT)\}

　　可以令s=i 2πf，得到FOH传递函数的拉普拉斯变换：

　　{\displaystyle H_{\mathrm{FOH}}(s)\,}{\displaystyle H_{\mathrm{FOH}}(s)\,}{\displaystyle={\mathcal{L}}\{h_{\mathrm{FOH}}(t)\}\}{\displaystyle={\mathcal{L}}\{h_{\mathrm{FOH}}(t)\}\}

　　{\displaystyle=\left({\frac{1-e^{-sT}}{sT}}\right)^{2}\}{\displaystyle=\left({\frac{1-e^{-sT}}{sT}}\right)^{2}\}

　　延迟一阶保持为因果系统。冲激响应在t小于0时没有值。

　　这类的延迟一阶保持可以用增益为H(z)=1−z−1的数字滤波器，将数字滤波器（x[n]−x[n−1]）的输出送到传统的数位类比转换器（本质上是零阶保持），再用H(s)=1/(sT)来积分DAC的输出。

预测型一阶保持

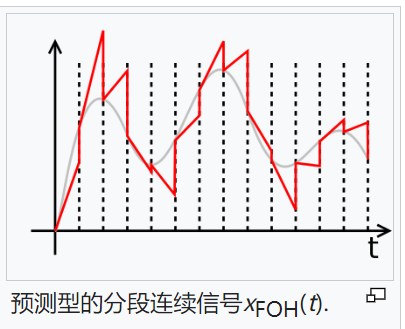
　　预测型一阶保持（predictive first-order hold）和上二一个一阶保持的差异较大，预测型一阶保持是因果系统的假想线性时不变系统，可以将理论取样信号

　　{\displaystyle x_{s}(t)\,}{\displaystyle x_{s}(t)\,}{\displaystyle=x(t)\T\sum _{n=-\infty}^{\infty}\delta(t-nT)\}{\displaystyle=x(t)\T\sum _{n=-\infty}^{\infty}\delta(t-nT)\}

　　{\displaystyle=T\sum _{n=-\infty}^{\infty}x(nT)\delta(t-nT)\}{\displaystyle=T\sum _{n=-\infty}^{\infty}x(nT)\delta(t-nT)\}

　　转换为分段线性输出信号，会用目前取样以及上一次的取様来线性外推下一个取样点，此滤波器的输出为

　　{\displaystyle x_{\mathrm{FOH}}(t)\,}{\displaystyle x_{\mathrm{FOH}}(t)\,}{\displaystyle=\sum _{n=-\infty}^{\infty}\left(x(nT)+\left(x(nT)-x((n-1)T)\right){\frac{t-nT}{T}}\right)\mathrm{rect}\left({\frac{t-nT}{T}}-{\frac{1}{2}}\right)\}{\displaystyle=\sum _{n=-\infty}^{\infty}\left(x(nT)+\left(x(nT)-x((n-1)T)\right){\frac{t-nT}{T}}\right)\mathrm{rect}\left({\frac{t-nT}{T}}-{\frac{1}{2}}\right)\}

　　{\displaystyle=\sum _{n=-\infty}^{\infty}x(nT)\left(\mathrm{rect}\left({\frac{t-nT}{T}}-{\frac{1}{2}}\right)-\mathrm{rect}\left({\frac{t-nT}{T}}-{\frac{3}{2}}\right)+\mathrm{tri}\left({\frac{t-nT}{T}}-1\right)\right)\}{\displaystyle=\sum _{n=-\infty}^{\infty}x(nT)\left(\mathrm{rect}\left({\frac{t-nT}{T}}-{\frac{1}{2}}\right)-\mathrm{rect}\left({\frac{t-nT}{T}}-{\frac{3}{2}}\right)+\mathrm{tri}\left({\frac{t-nT}{T}}-1\right)\right)\}

　　其等效冲激响应为

　　{\displaystyle h_{\mathrm{FOH}}(t)\,}{\displaystyle h_{\mathrm{FOH}}(t)\,}{\displaystyle={\frac{1}{T}}\left(\mathrm{rect}\left({\frac{t}{T}}-{\frac{1}{2}}\right)-\mathrm{rect}\left({\frac{t}{T}}-{\frac{3}{2}}\right)+\mathrm{tri}\left({\frac{t}{T}}-1\right)\right)\}{\displaystyle={\frac{1}{T}}\left(\mathrm{rect}\left({\frac{t}{T}}-{\frac{1}{2}}\right)-\mathrm{rect}\left({\frac{t}{T}}-{\frac{3}{2}}\right)+\mathrm{tri}\left({\frac{t}{T}}-1\right)\right)\}

　　{\displaystyle={\begin{cases}{\frac{1}{T}}\left(1+{\frac{t}{T}}\right)&{\mbox{if}}0\leq t<T\\{\frac{1}{T}}\left(1-{\frac{t}{T}}\right)&{\mbox{if}}T\leq t<2T\\0&{\mbox{otherwise}}\end{cases}}\}{\displaystyle={\begin{cases}{\frac{1}{T}}\left(1+{\frac{t}{T}}\right)&{\mbox{if}}0\leq t<T\\{\frac{1}{T}}\left(1-{\frac{t}{T}}\right)&{\mbox{if}}T\leq t<2T\\0&{\mbox{otherwise}}\end{cases}}\}

　　其中{\displaystyle\mathrm{rect}(x)\}{\displaystyle\mathrm{rect}(x)\}为矩形函数，而{\displaystyle\mathrm{tri}(x)\}{\displaystyle\mathrm{tri}(x)\}为三角形函数。

　　等效频率响应为冲激响应的傅里叶变换。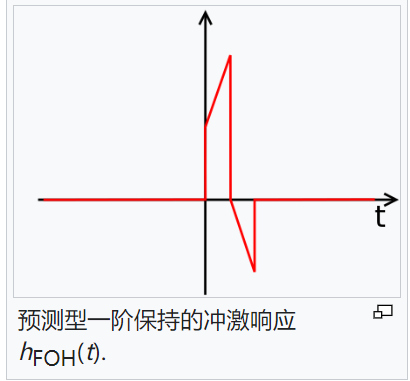

　　{\displaystyle H_{\mathrm{FOH}}(f)\,}{\displaystyle H_{\mathrm{FOH}}(f)\,}{\displaystyle={\mathcal{F}}\{h_{\mathrm{FOH}}(t)\}\}{\displaystyle={\mathcal{F}}\{h_{\mathrm{FOH}}(t)\}\}

　　{\displaystyle=(1+i2\pi fT)\left({\frac{1-e^{-i2\pi fT}}{i2\pi fT}}\right)^{2}\}{\displaystyle=(1+i2\pi fT)\left({\frac{1-e^{-i2\pi fT}}{i2\pi fT}}\right)^{2}\}

　　{\displaystyle=(1+i2\pi fT)e^{-i2\pi fT}\mathrm{sinc}^{2}(fT))\}{\displaystyle=(1+i2\pi fT)e^{-i2\pi fT}\mathrm{sinc}^{2}(fT))\}

　　其中{\displaystyle\mathrm{sinc}(x)\}{\displaystyle\mathrm{sinc}(x)\}为Sinc函数。

　　可以令s=i 2πf，得到FOH传递函数的拉普拉斯变换]：

　　{\displaystyle H_{\mathrm{FOH}}(s)\,}{\displaystyle H_{\mathrm{FOH}}(s)\,}{\displaystyle={\mathcal{L}}\{h_{\mathrm{FOH}}(t)\}\}{\displaystyle={\mathcal{L}}\{h_{\mathrm{FOH}}(t)\}\}

　　{\displaystyle=(1+sT)\left({\frac{1-e^{-sT}}{sT}}\right)^{2}\}{\displaystyle=(1+sT)\left({\frac{1-e^{-sT}}{sT}}\right)^{2}\}

　　此为因果系统。预测型一阶保持的冲激响应不会在输入脉冲之前就出现。

　　这种分段线性的重建信号方式可以用增益H(z)=1−z−1</sup的数字滤波器来实现，将数位滤波器的输出（就是x[n]−x[n−1]）接到理想的传统数位类比转换器（其本质上是零阶保持），将其输出接到类比滤波器，其传递函数为H(s)=(1+sT)/(sT)。