漏电感，或漏感（英语：Leakage inductance）源于不完全耦合的变压器，是变压器中初级线圈与次级线圈的耦合系数小于1，变压器部分线圈不会有变压作用，只有类似抑流电感的作用，这部分线圈的电感即为漏电感。

　　若初级线圈与次级线圈完全耦合（耦合系数k=1）为理想的变压器时，漏电感的数值为零。但一般变压器的耦合系数多为1以下，因为未完全耦合，所以线圈的大部分有变压器的功能、有一部分具有电感的功能。在等效电路上，漏电感指的是与变压器的初级线圈或次级线圈与Choke Coil Le以串联方式连接。漏电感的定义有电气学会及工业会测量法的两种定义。

漏电感的产生

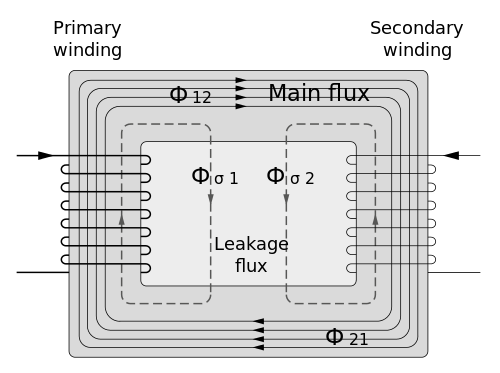
变压器的磁通

　　变压器中与初级侧线圈及次级侧线圈两者皆互连的磁通称为互磁通（或主磁通，Φ12或Φ21）。变压器的磁通除此之外，还有仅与初级侧线圈互连而未与次级侧线圈互连的初级侧漏磁通（或自磁通Φσ1），仅与次级侧线圈互连而未与初级侧线圈互连的次级侧漏磁通（Φσ2）。理想的变压器中只会有互磁通，但实际上因为变压器中有磁气外漏所以一定会有漏磁通的存在。且因为漏磁通仅是与初级侧线圈，次级侧线圈任一方交链，也就是意味着这是各线圈的电感附加在其中。因此，初级侧漏磁通为初级侧漏电感，次级侧漏磁通为次级侧漏电感。

　　耦合系数k，初级线圈的自感为L1，次级线圈的自感为L2，则各漏电感为：

　　{\displaystyle L_{\mathrm{e1}}=(1-k)\cdot L_{\mathrm{1}}\,}{\displaystyle L_{\mathrm{e1}}=(1-k)\cdot L_{\mathrm{1}}\,}

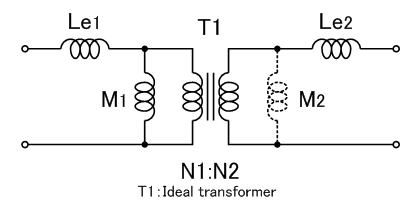
　　{\displaystyle L_{\mathrm{e2}}=(1-k)\cdot L_{\mathrm{2}}\,}{\displaystyle L_{\mathrm{e2}}=(1-k)\cdot L_{\mathrm{2}}\,}

三端子等效电路

　　变压器的等效电路中漏电感在初级侧或次级侧中透过理想的变压器变换为阻抗，亦被记载为相互电感:互感，这就是三端子等效电路。以三端子等效电路表示的变压器的等效电路中，初级侧漏电感Le1与次级侧漏电感Le2为相同数值，这是电气学会定义的漏电感。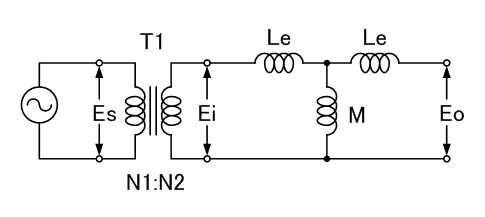

实际测量漏电感（短路电感）

　　工业会中实际测量所制定的漏电感Lk为将变压器的初级线圈或次级线圈短路，测量另一方所得，此Lk即为工业会实际测量（工业标准）所得的漏电感，与电气学会定义的漏电感数值不同。这Lk是被称于其他国家工业标准的短路电感(short circuit inductance Lsc[6]或Kurzschlussinduktivität Lk)。

　　实际测量Löffnen及Lkurz可得耦合系数k：

　　{\displaystyle k={\sqrt{1-{\frac{L_{kurz}}{L_{offnen}}}}}}{\displaystyle k={\sqrt{1-{\frac{L_{kurz}}{L_{offnen}}}}}}

　　将次级侧短路测量初级侧所得的电感称为初级侧漏电感Lk1，将初级侧短路测量次级侧所得的电感称为次级侧漏电感Lk2。利用这些数值与各自的线圈的自感，算出的耦合系数k，在初级侧及次级侧所测量到的数值必须完全相同[9][10]。

L等效电路（简易等效电路）

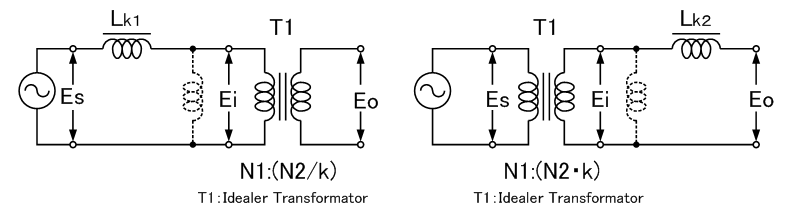
　　较为实用的表示方式是将漏电感整合在初级侧或次级侧。等效电路中不管将漏电感配置在初级侧或次级侧，根据其线圈数比（变成比）会与阻抗变换值相同：

　　{\displaystyle L_{\mathrm{k2}}=L_{\mathrm{k1}}\cdot\left({\frac{N_{2}}{N_{1}}}\right)^{2}}{\displaystyle L_{\mathrm{k2}}=L_{\mathrm{k1}}\cdot\left({\frac{N_{2}}{N_{1}}}\right)^{2}}

　　{\displaystyle L_{\mathrm{k1}}=L_{\mathrm{k2}}\cdot\left({\frac{N_{1}}{N_{2}}}\right)^{2}}{\displaystyle L_{\mathrm{k1}}=L_{\mathrm{k2}}\cdot\left({\frac{N_{1}}{N_{2}}}\right)^{2}}

　　此时，若漏电感Lk与变压器的初级线圈或次级线圈与Choke Coil Le以串联方式连接则会有等效的功能。在设计电路上，工业会中实际测量所得的漏电感[11]较具实用性。

　　各自的线圈的自感L1，L2与工业会中实际测量且定义的漏电感的关系如下：

　　{\displaystyle L_{\mathrm{k1}}=(1-k^{2})\cdot L_{\mathrm{1}}\,}{\displaystyle L_{\mathrm{k1}}=(1-k^{2})\cdot L_{\mathrm{1}}\,}

　　{\displaystyle L_{\mathrm{k2}}=(1-k^{2})\cdot L_{\mathrm{2}}\,}{\displaystyle L_{\mathrm{k2}}=(1-k^{2})\cdot L_{\mathrm{2}}\,}

补充

　　工业会中实际测量且定义的漏电感Lk与电气学会定义的漏电感Le的关系如下：

　　{\displaystyle L_{\mathrm{k1}}=(1+k)\cdot L_{\mathrm{e1}}\,}{\displaystyle L_{\mathrm{k1}}=(1+k)\cdot L_{\mathrm{e1}}\,}

　　{\displaystyle L_{\mathrm{k2}}=(1+k)\cdot L_{\mathrm{e2}}\,}{\displaystyle L_{\mathrm{k2}}=(1+k)\cdot L_{\mathrm{e2}}\,}

利用漏电感

　　一般变压器的漏电感因为会导致变压器输出电压降低，所以较不为乐见，但可积极利用电流通过时电压下降的特性，使变压器有较大的漏电感，主要可应用在具有负性阻抗特性的萤光灯，霓虹灯，以及其他的放电灯的电流镇流器，弧形溶接的镇流器，微波炉的微波真空管的镇流器等。漏磁变压器，谐振变压器的用途非常多。

　　此外，次级线圈中与谐振电容并联，使次级侧的漏电感，电容成分产生谐振的谐振变压器可应用在萤光灯电子式镇流器（Inverter），霓虹灯电子镇流器，冷阴极管Inverter或特斯拉线圈中。