电荷泵锁相回路（Charge-pump phase-locked loop）简称CP-PLL，是一种鉴相器适用于方波输入信号的锁相回路。CP-PLL可以快速的锁定到输入信号的相位，可以达到很低的稳态相位误差。

鉴相器（PFD）

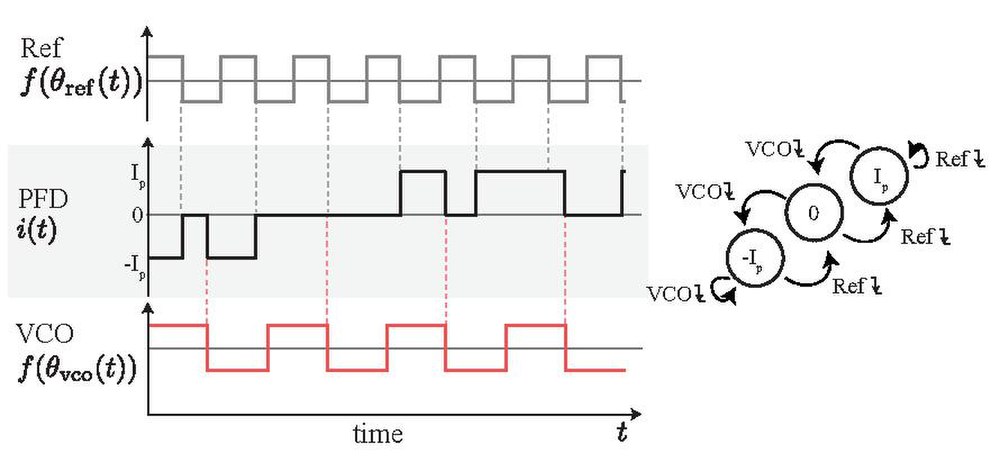
　　鉴相器（PFD）是由参考信号（Ref）以及受控输出（VCO）信号的下缘所触发。PFD{\displaystyle i(t)}i(t)的输出信号只有三个状态：0,{\displaystyle+I_{p}}{\displaystyle+I_{p}},和{\displaystyle-I_{p}}{\displaystyle-I_{p}}。参考信号的下缘会使PFD切换到较高的状态，若PFD已经在{\displaystyle+I_{p}}{\displaystyle+I_{p}}就不会变动。VCO信号的下缘会使PFD切换到较低的状态，若PFD已经在{\displaystyle-I_{p}}{\displaystyle-I_{p}}就不会变动。若二个信号的下缘同时出现，PFD会切换到0。

CP-PLL的数学模型

　　第一个二阶CP-PLL的数学模型是由佛洛依德·加德纳在1980年提出的。M.van Paemel在1994年提出了不考虑VCO过载（overload）的非线性模型[3]，N.Kuznetsov等人在2019年优化该模型。也有学者在推导考虑VCO过载的CP-PLL解析解数学模型。

　　CP-PLL的数学模型可以针对一些参数进行解析的预估，例如hold-in范围（在VCO没有过载的情形下，可能进行锁相的输入信号频率范围），及捕获范围（pull-in range，在CP-PLL任意初始状态下，CP-PLL最终可以锁相的输入信号频率范围）。

二阶CP-PLL的连续时间线性模型以及加德纳的猜想

　　加德纳的分析是以以下的近似为基础：每个参考信号的周期内，PFD非零的时间区间为

　　{\displaystyle t_{p}=|\theta _{e}|/\omega _{\rm{ref}},\\theta _{e}=\theta _{\rm{ref}}-\theta _{\rm{vco}}.}{\displaystyle t_{p}=|\theta _{e}|/\omega _{\rm{ref}},\\theta _{e}=\theta _{\rm{ref}}-\theta _{\rm{vco}}.}

　　CP-PLL的PDF平均输出为

　　{\displaystyle i_{d}=I_{p}\theta _{e}/2\pi}{\displaystyle i_{d}=I_{p}\theta _{e}/2\pi}

　　对应的传递函数为

　　{\displaystyle I_{d}(s)=I_{p}\theta _{e}(s)/2\pi}{\displaystyle I_{d}(s)=I_{p}\theta _{e}(s)/2\pi}

　　若用滤波器传递函数{\displaystyle F(s)=R+{\frac{1}{Cs}}}{\displaystyle F(s)=R+{\frac{1}{Cs}}}以及VCO传递函数{\displaystyle\theta _{\rm{vco}}(s)=K_{\rm{vco}}I_{d}(s)F(s)/s}{\displaystyle\theta _{\rm{vco}}(s)=K_{\rm{vco}}I_{d}(s)F(s)/s}，可以得到加德纳的二阶CP-PLL线性近似平均模型:

　　{\displaystyle{\frac{\theta _{e}(s)}{\theta _{\rm{ref}}(s)}}={\frac{2\pi s}{2\pi s+K_{\rm{vco}}I_{p}\left(R+{\frac{1}{Cs}}\right)}}.}{\displaystyle{\frac{\theta _{e}(s)}{\theta _{\rm{ref}}(s)}}={\frac{2\pi s}{2\pi s+K_{\rm{vco}}I_{p}\left(R+{\frac{1}{Cs}}\right)}}.}

　　佛洛依德·加德纳在1980年以上述的理解，提出了猜想：“实际电荷泵锁相回路的暂态响应，预期会和等效传统PLL的暂态响应几乎相同。”:1856（加德纳对CP-PLL的猜想）。依照加德纳的结果，也类似Egan在type 2 APLL捕获范围的猜想，Amr M.Fahim在其书中猜想[7]:6：为了要达到无限大的捕获范围，CP-PLL的回路滤波器需要使用主动滤波器（Fahim-Egan在type II CP-PLL捕获范围的猜想）。

二阶CP-PLL的连续时间非线性模型

　　为了简化推导，但不失去通用性，假设VCO和参考信号在其相位为整数时为其下降缘。令参考信号第一个下降缘的时间为{\displaystyle t=0}t=0。PFD状态{\displaystyle i(0)}{\displaystyle i(0)}会依PFD的初始状态{\displaystyle i(0-)}{\displaystyle i(0-)}，VCO的初始相位移{\displaystyle\theta _{vco}(0)}{\displaystyle\theta _{vco}(0)}，以及参考信号{\displaystyle\theta _{ref}(0)}{\displaystyle\theta _{ref}(0)}的值而不同。

　　若利用电阻和电容制作纯PI（比例积分）的滤波器，其输入电流{\displaystyle i(t)}i(t)和输出电压{\displaystyle v_{F}(t)}{\displaystyle v_{F}(t)}的关系为

　　{\displaystyle{\begin{aligned}v_{F}(t)=v_{c}(0)+Ri(t)+{\frac{1}{C}}\int\limits _{0}^{t}i(\tau)d\tau\end{aligned}}}{\displaystyle{\begin{aligned}v_{F}(t)=v_{c}(0)+Ri(t)+{\frac{1}{C}}\int\limits _{0}^{t}i(\tau)d\tau\end{aligned}}}

　　其中{\displaystyle R>0}{\displaystyle R>0}是电阻，{\displaystyle C>0}{\displaystyle C>0}是电感。{\displaystyle v_{c}(t)}{\displaystyle v_{c}(t)}是电容器的电压。控制信号{\displaystyle v_{F}(t)}{\displaystyle v_{F}(t)}会调整VCO频率：

　　{\displaystyle{\begin{aligned}{\dot{\theta}}_{vco}(t)=\omega _{vco}(t)=\omega _{vco}^{\text{free}}+K_{vco}v_{F}(t),\end{aligned}}}{\displaystyle{\begin{aligned}{\dot{\theta}}_{vco}(t)=\omega _{vco}(t)=\omega _{vco}^{\text{free}}+K_{vco}v_{F}(t),\end{aligned}}}

　　其中{\displaystyle\omega _{vco}^{\text{free}}}{\displaystyle\omega _{vco}^{\text{free}}}是VCO的自由运行频率（也就是{\displaystyle v_{F}(t)\equiv 0}{\displaystyle v_{F}(t)\equiv 0})，{\displaystyle K_{vco}}{\displaystyle K_{vco}}是VCO增益（灵敏度）、{\displaystyle\theta _{vco}(t)}{\displaystyle\theta _{vco}(t)}是VCO相位。最后，CP-PLL连续时间非线性数学模型如下

　　{\displaystyle{\begin{aligned}{\dot{v}}_{c}(t)={\tfrac{1}{C}}i(t),\quad{\dot{\theta}}_{vco}(t)=\omega _{vco}^{\text{free}}+K_{vco}(Ri(t)+v_{c}(t))\end{aligned}}}{\displaystyle{\begin{aligned}{\dot{v}}_{c}(t)={\tfrac{1}{C}}i(t),\quad{\dot{\theta}}_{vco}(t)=\omega _{vco}^{\text{free}}+K_{vco}(Ri(t)+v_{c}(t))\end{aligned}}}

　　其中有以下的不连续分段常数非线性

　　{\displaystyle i(t)=i{\big(}i(t-),\theta _{ref}(t),\theta _{vco}(t){\big)}}{\displaystyle i(t)=i{\big(}i(t-),\theta _{ref}(t),\theta _{vco}(t){\big)}}

　　初始条件为{\displaystyle{\big(}v_{c}(0),\theta _{vco}(0){\big)}}{\displaystyle{\big(}v_{c}(0),\theta _{vco}(0){\big)}}.此模型是非线性、非自主式、不连续的开关系统。

二阶CP-PLL的离散时间非线性模型

　　假设参考信号频率为常数:{\displaystyle\theta _{ref}(t)=\omega _{ref}t={\frac{t}{T_{ref}}},}{\displaystyle\theta _{ref}(t)=\omega _{ref}t={\frac{t}{T_{ref}}},}其中{\displaystyle T_{ref}}{\displaystyle T_{ref}}、{\displaystyle\omega _{ref}}{\displaystyle\omega _{ref}}和{\displaystyle\theta _{ref}(t)}{\displaystyle\theta _{ref}(t)}是参考资料的周期、频率和相位。

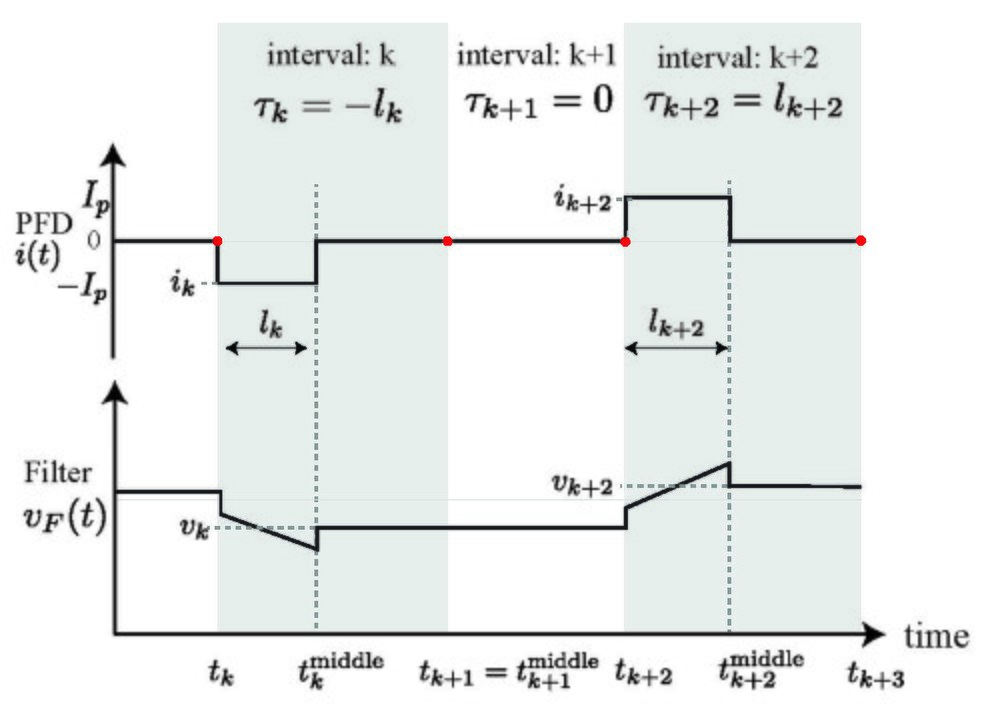
　　令{\displaystyle t_{0}=0}{\displaystyle t_{0}=0}，这表示{\displaystyle t_{0}^{\rm{middle}}}{\displaystyle t_{0}^{\rm{middle}}}是第一个PFD输出为0的时间（若{\displaystyle i(0)=0}{\displaystyle i(0)=0}，则{\displaystyle t_{0}^{\rm{middle}}=0}{\displaystyle t_{0}^{\rm{middle}}=0}）且{\displaystyle t_{1}}t_{1}是VCO或参考信号的第一个下降缘。其且，可以定义对应的递减数列{\displaystyle\{t_{k}\}}{\displaystyle\{t_{k}\}}、{\displaystyle\{t_{k}^{\rm{middle}}\}}{\displaystyle\{t_{k}^{\rm{middle}}\}}，其中{\displaystyle k=0,1,2...}{\displaystyle k=0,1,2...}。

　　令{\displaystyle t_{k}<t_{k}^{\rm{middle}}}{\displaystyle t_{k}<t_{k}^{\rm{middle}}}.则在{\displaystyle t\in[t_{k},t_{k}^{\rm{middle}})}{\displaystyle t\in[t_{k},t_{k}^{\rm{middle}})}时，{\displaystyle{\text{sign}}(i(t))}{\displaystyle{\text{sign}}(i(t))}是非零的常数（{\displaystyle\pm 1}{\displaystyle\pm 1}）。令{\displaystyle\tau _{k}}{\displaystyle\tau _{k}}为PFD脉波宽度（PFD输出为非零长度的时间区间）乘以PFD输出的正负号：

　　{\displaystyle\tau _{k}=(t_{k}^{\rm{middle}}-t_{k}){\text{sign}}(i(t))}{\displaystyle\tau _{k}=(t_{k}^{\rm{middle}}-t_{k}){\text{sign}}(i(t))}for{\displaystyle t\in[t_{k},t_{k}^{\rm{middle}})}{\displaystyle t\in[t_{k},t_{k}^{\rm{middle}})}

　　{\displaystyle\tau _{k}=0}{\displaystyle\tau _{k}=0}for{\displaystyle t_{k}=t_{k}^{\rm{middle}}}{\displaystyle t_{k}=t_{k}^{\rm{middle}}}

　　若VCO的下降缘在参考信号的下降缘之前，则{\displaystyle\tau _{k}<0}{\displaystyle\tau _{k}<0}，反之，可得{\displaystyle\tau _{k}>0}{\displaystyle\tau _{k}>0}。{\displaystyle\tau _{k}}{\displaystyle\tau _{k}}可以看出二个信号下降缘的先后顺序。在{\displaystyle(t_{k}^{\rm{middle}},t_{k+1})}{\displaystyle(t_{k}^{\rm{middle}},t_{k+1})}区间内，PFD输出为零，PFD{\displaystyle i(t)\equiv 0}{\displaystyle i(t)\equiv 0}：

　　{\displaystyle v_{F}(t)\equiv v_{k}}{\displaystyle v_{F}(t)\equiv v_{k}}for{\displaystyle t\in[t_{k}^{\rm{middle}},t_{k+1})}{\displaystyle t\in[t_{k}^{\rm{middle}},t_{k+1})}.

　　将{\displaystyle(\tau _{k},v_{k})}{\displaystyle(\tau _{k},v_{k})}变成下式的变数变换[8]{\displaystyle p_{k}={\frac{\tau _{k}}{T_{\rm{ref}}}},u_{k}=T_{\rm{ref}}(\omega _{\rm{vco}}^{\text{free}}+K_{\rm{vco}}v_{k})-1,}{\displaystyle p_{k}={\frac{\tau _{k}}{T_{\rm{ref}}}},u_{k}=T_{\rm{ref}}(\omega _{\rm{vco}}^{\text{free}}+K_{\rm{vco}}v_{k})-1,}可以让参数减至二个：{\displaystyle\alpha=K_{\rm{vco}}I_{p}T_{\rm{ref}}R,\beta={\frac{K_{\rm{vco}}I_{p}T_{\rm{ref}}^{2}}{2C}}.}{\displaystyle\alpha=K_{\rm{vco}}I_{p}T_{\rm{ref}}R,\beta={\frac{K_{\rm{vco}}I_{p}T_{\rm{ref}}^{2}}{2C}}.}

　　此处{\displaystyle p_{k}}p_k是正规化的相位偏移，{\displaystyle u_{k}+1}{\displaystyle u_{k}+1}是VCO频率{\displaystyle\omega _{\rm{vco}}^{\text{free}}+K_{\rm{vco}}v_{k}}{\displaystyle\omega _{\rm{vco}}^{\text{free}}+K_{\rm{vco}}v_{k}}相对于参考频率{\displaystyle{\frac{1}{T_{\rm{ref}}}}}{\displaystyle{\frac{1}{T_{\rm{ref}}}}}的比例。

　　最后，不考虑VCO过载的二阶CP-PLL离散时间模型如下

　　{\displaystyle{\begin{aligned}&u_{k+1}=u_{k}+2\beta p_{k+1},\\&p_{k+1}={\begin{cases}{\frac{-(u_{k}+\alpha+1)+{\sqrt{(u_{k}+\alpha+1)^{2}-4\beta c_{k}}}}{2\beta}},\quad{\text{for}}p_{k}\geq 0,\quad c_{k}\leq 0,\\{\frac{1}{u_{k}+1}}-1+(p_{k}{\text{mod}}1),\quad{\text{for}}p_{k}\geq 0,\quad c_{k}>0,\\l_{k}-1,\quad{\text{for}}p_{k}<0,\quad l_{k}\leq 1,\\{\frac{-(u_{k}+\alpha+1)+{\sqrt{(u_{k}+\alpha+1)^{2}-4\beta d_{k}}}}{2\beta}},\quad{\text{for}}p_{k}<0,\quad l_{k}>1,\end{cases}}\end{aligned}}}{\displaystyle{\begin{aligned}&u_{k+1}=u_{k}+2\beta p_{k+1},\\&p_{k+1}={\begin{cases}{\frac{-(u_{k}+\alpha+1)+{\sqrt{(u_{k}+\alpha+1)^{2}-4\beta c_{k}}}}{2\beta}},\quad{\text{for}}p_{k}\geq 0,\quad c_{k}\leq 0,\\{\frac{1}{u_{k}+1}}-1+(p_{k}{\text{mod}}1),\quad{\text{for}}p_{k}\geq 0,\quad c_{k}>0,\\l_{k}-1,\quad{\text{for}}p_{k}<0,\quad l_{k}\leq 1,\\{\frac{-(u_{k}+\alpha+1)+{\sqrt{(u_{k}+\alpha+1)^{2}-4\beta d_{k}}}}{2\beta}},\quad{\text{for}}p_{k}<0,\quad l_{k}>1,\end{cases}}\end{aligned}}}

　　其中

　　{\displaystyle{\begin{aligned}c_{k}=(1-(p_{k}{\text{mod}}1))(u_{k}+1)-1,S_{l_{k}}=-(u_{k}-\alpha+1)p_{k}+\beta p_{k}^{2},l_{k}={\frac{1-(S_{l_{k}}{\text{mod}}1)}{u_{k}+1}},d_{k}=(S_{l_{k}}{\text{mod}}1)+u_{k}.\end{aligned}}}{\displaystyle{\begin{aligned}c_{k}=(1-(p_{k}{\text{mod}}1))(u_{k}+1)-1,S_{l_{k}}=-(u_{k}-\alpha+1)p_{k}+\beta p_{k}^{2},l_{k}={\frac{1-(S_{l_{k}}{\text{mod}}1)}{u_{k}+1}},d_{k}=(S_{l_{k}}{\text{mod}}1)+u_{k}.\end{aligned}}}

　　此离散时间模型只在{\displaystyle(u_{k}=0,p_{k}=0)}{\displaystyle(u_{k}=0,p_{k}=0)}有一个稳态，可以估计hold-in范围和捕获范围。

　　若VCO过载，也就是{\displaystyle{\dot{\theta}}_{\rm{vco}}(t)}{\displaystyle{\dot{\theta}}_{\rm{vco}}(t)}为零，或者是以下的式子{\displaystyle(p_{k}>0,u_{k}<2\beta p_{k}-1)}{\displaystyle(p_{k}>0,u_{k}<2\beta p_{k}-1)}或{\displaystyle(p_{k}<0,u_{k}<\alpha-1)}{\displaystyle(p_{k}<0,u_{k}<\alpha-1)},则需要考虑额外的CP-PLL动态特性[5]。针对任何参数，只要VCO和参考信号的频率差够大，就会使VCO过载。在实务上，需避免VCO的过载。

高阶CP-PLL的非线性模型

　　高阶CP-PLL非线性模型推导和超越方程有关，无法求得解析解，需要用近似的方式计算